Rational agents can be uncertain about what is objectively valuable. Former CPNSS visitor Luca Zanetti shows how the debate on model uncertainty in science is relevant to the debate on moral uncertainty in normative ethics. This offers new ways of managing moral uncertainty.

We can be uncertain not only about natural and social phenomena, or because our knowledge of these phenomena is limited, but also about what is (objectively) valuable.

Here is an example. You have a choice between option A and option B. You’d rather choose A than B. However, you are still determining the moral value of these options. According to one of the two moral views that you hold, A and B are both permissible, but according to the other view, only B is permissible. You are uncertain about which of these two views is correct, and therefore, you don’t know which one to choose. 

In this post, I will compare this moral uncertainty in ethics with model uncertainty in science. The analogy between moral and model uncertainty can be introduced by considering the standard definition of the expected utility of an option as being the average of the values of the possible outcomes with each being weighted by the probability that the outcome occurs if the agent chooses that option. Rational agents should maximise their expected utility in conditions of uncertainty. However, there are two practical limitations to this principle. First, the agent may not have enough evidence to assign precise probabilities to the outcomes. Second, the agent may not have enough experience to attribute a determinate value to these outcomes. Despite this analogy, decision theories often treat these two types of uncertainty differently.

Maximising Expected Choiceworthiness

Recently, a number of philosophers have argued that if we are uncertain about what we (morally) ought to do, then we should choose the option with the highest expected choiceworthiness. The choiceworthiness of an option corresponds to how much the option is worthy from the point of view of a particular moral theory. We then assign a probability to each moral theory representing the agent’s degree of belief or credence that the theory is correct. The expected choiceworthiness of an option is the average of its moral values each weighted by the agent’s credence.

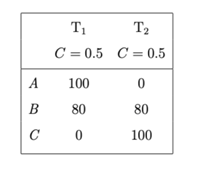
Imagine that the agent has to choose between three options, A, B and C. The agent is uncertain about which of the following two moral theories is correct. According to the first theory, A’s choiceworthiness is 100, B’s choiceworthiness is 80, and C’s choiceworthiness is 0. According to the second theory, by contrast, B’s choiceworthiness is still 80, but C’s choiceworthiness is 100 and A’s choiceworthiness is 0. The agent decides to split their confidence equally between these two theories, assigning a probability of 50% to each. If the agent maximises the expected moral value, then they should choose option B. This minimises the risk of choosing an option that is objectively the worst option (assuming that one of the two theories is correct).

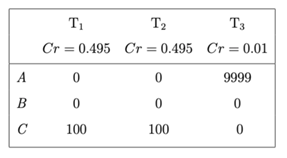
However, let’s now consider the following case. This time the agent has 0.495 credence that theory T1 is correct, and 0.495 credence that T2 is correct. According to both T1 and T2, A and B have a value of zero, while C has a value of a hundred. Therefore, the agent should be very confident that the value of C is greater than the value of both A and B. However, the agent becomes acquainted with a third theory, T3. According to T3, the value of A is much greater (say, 9.999). The agent’s credence in the third theory is very low (1%). However, the expected choiceworthiness of A is 9.999 * 0.01 = 99,99, whereas the expected choiceworthiness of C is 100 * 0.495 +  100 * 0.495 = 99. They should therefore choose option A, even if both moral theories in which the agent has the most confidence in – namely, T1 and T2 – agree that A has no moral value, the agent’s credence in T3 is very small, and C is better than A according to both T1 and T2.   

Empirical Uncertainty and Moral Uncertainty

The principle of expected choiceworthiness maximisation has often been supported using an analogy between moral uncertainty and empirical uncertainty: if maximising utility value is often the rational thing to do in conditions of empirical uncertainty, then maximising the expected moral value is what we ought to do when we face moral uncertainty. Empirical uncertainty is uncertainty related to the states of the world. For example, we can be uncertain about the result of two rolls of a dice. Two arguments have been brought to defend this analogy (both of which appear in MacAskill, Bykvist and Ord’s recent book on moral uncertainty). 

The first argument starts from the fact that we can be uncertain not only about empirical and moral matters but also about the nature of our own uncertainty. For example, we may be uncertain if we should choose the lobster or a vegetarian meal because we don’t know if the suffering of non-human animals is morally relevant, but we may also not know if we lack some knowledge about the physiology of the lobster, or if our moral theories are in a sense incomplete and therefore don’t cover all of the cases. If our attitudes towards empirical uncertainty and towards moral uncertainty were different, then it would make sense to spend time figuring out if our uncertainty is empirical or moral. 

This is not really convincing. Moral uncertainty is plausibly a form of uncertainty that is due to lack of information, insufficient understanding, or cognitive limitations, and uncertainties of this kind can usually be reduced over time as more information is collected. However, there is a question of whether the described situation is even possible. As it is usually presented, moral uncertainty is uncertainty about which moral views are correct. Therefore it seems that if I don’t know if I should order lobster or the vegetarian meal because I believe conflicting moral theories, I must be aware of what these theories are and what they prescribe. Of course, moral uncertainty can have different sources (for example, I can have meta-theoretical uncertainty about the completeness of my moral theories). But a morally uncertain agent in the relevant sense should be able to determine how much of their uncertainty is moral. 

The second argument is that the distinction between moral and empirical uncertainty is arbitrary as far as decision theory is concerned. Our uncertainty may concern different (for example, natural or social) worldly states, and we still think that maximising the expected value is often the rational thing to do in all these cases. It would be odd if only moral uncertainty rationally mandated a different attitude. However, it sometimes makes sense to distinguish between different kinds of uncertainties: for example, aleatoric uncertainties and epistemic uncertainties are often treated differently in risk analysis. Moreover, moral uncertainty is not the only exception to the rule unless (1) there are no other cases of uncertainty that are plausibly analogous to moral uncertainty, and (2) for which a different rational attitude is warranted. I will now suggest that at least some moral uncertainties should instead be understood as model risks, and, therefore, that our attitudes to the two kinds of uncertainty should be the same. 

Intertheoretic Comparisons of Value

Models risks are caused by our use of mathematical models. These risks are usually due to two types of uncertainty. On the one hand, there are model uncertainties that concern the form of the equations that we use to model natural and social phenomena. On the other hand, there are parametric uncertainties that concern the value of the parameters in these equations. For example, we can be uncertain if the model includes all the relevant explanatory variables. This is a case of model uncertainty. At the same time, we can be relatively confident that the model is correct but uncertain as to whether the values of its parameters have been measured correctly. This is a case of parametric uncertainty.

There is a growing discussion on the use of formal models in ethics. Some defend the view that moral theories are models, or, at least, that models are necessary in order to apply the theory. No matter what one thinks of this, there is a particular use of formal models that has so far been neglected, that is, the use of these models as tools to compare the value of the same option across different theories in cases of moral uncertainty. I will give two examples: (a) models that are used to compare ‘merely ordinal’ moral theories, and (b) models that are used to compare ‘interval-scale’moral theories. 

(a) A merely ordinal moral theory induces a partial order among the options but fails to determine how any two options compare with each other. For example, the theory may imply that B is better than A and C is better than A, but not whether B is better than C or vice versa. These cases are of great practical importance since theories claiming that some goods are incommensurable are typically merely ordinal theories. When a theory is merely ordinal, the maximisation rule is not wrong but unavailable.

In this case, moral uncertainty can be handled using voting rules. Value theories are modelled as voters that express a set of pairwise preferences among options. This theories-as-voters model involves different kinds of idealisations, analogously to scientific models. On the one hand, the model idealises away from any information provided by the theory beyond the order. Therefore, the model treats all theories as ordinal. This also involves a distortion of the phenomenon, since moral theories differ from voters in relevant respects. For example, many voting rules allow for strategic voting, but the very idea of strategic voting does not seem to make sense in the case of moral theories. At the same time, the model allows importing information from social choice theory to solve the problem of intertheoretic comparisons of values. An example is the choice of the option with the smaller biggest pairwise defeat (the Simpon-Kramer method). However, the agent can be unsure about which voting rule should be used in a specific situation.

(b) An interval-scale theory provides the ratios between the moral values of the options. For example, the first theory may assert that A is ten times better than B, whereas the second theory claims that B is a hundred times better than A. To compare the two theories, we can use a single-scale model in which these theories can be compared on a single scale of moral value. Constructing a single-scale model amounts to finding a normalisation. This does not mean that the theories are in fact comparable; if it turns out that they are not, then the existence of a single-scale model is a distorting idealisation of the model. Different normalisation methods have been proposed. Two examples are Lockhart’s Principle of Equity among Moral Theories (PEMT), according to which the minimum value and the maximum value are the same across all theories, and MacAskill, Bykvist and Ord’s Variance Voting, according to which the variance is the same across moral theories. Again, the agent can be uncertain about which method should be used in a given situation.

As of today, there is no agreement on what should be our response to model uncertainty. The idea that probabilities can represent model uncertainty can be challenged. To give just one example, the Intergovernmental Panel on Climate Change (IPCC) has gradually shifted to express uncertainty using qualitative levels of confidence (very low, low, medium, high, and very high) rather than precise probabilities. According to some decision theorists maximising the expected value using the mean estimate produced by the models is not the right thing to do, and we should instead use different rules, for example, considering only the estimates that we hold with a level of confidence that is appropriate for what is at stake in the decision situation. More generally, representations of model uncertainty in economics often allow for the attitudes towards empirical uncertainty and model risk to be different. 

This can have consequences for how we think about moral uncertainty. Imagine that an agent is risk neutral in conditions of empirical uncertainty, but very averse to model risks. For this reason, the agent relies on a plurality of models, e.g. PEMT and variance voting, and chooses an option that does sufficiently well for a reasonable array of these models. For example, an option can be safer than others because its value is reasonably stable across different models. By contrast, the ‘risky’ options whose value is extremely high according to some low-credence but high-stakes theory can be discarded because its expected choice-worthiness is very sensitive to which normalisation method is used. If the agent’s response to moral and model uncertainty are the same, then this agent will make more prudent decisions than they would do if they maximised expected choice-worthiness.

Conclusions

In summary, there are two ways in which the philosophical debate about model uncertainty can inform the debate on moral uncertainty. The first is by highlighting that agents may face not only uncertainty about which moral theory is correct but also uncertainty about the formal models that are used to compare these theories with each other. The second contribution is to offer new ways of managing moral uncertainty. The answer may depend on how we conceive moral uncertainty. Many philosophers have claimed that the response to both empirical uncertainty and moral uncertainty should be the same. I suggest that at least some moral uncertainties should instead be treated in the same way as model risks. In this respect, we can learn much about how to face moral uncertainty by exploring how we should make decisions using ensembles of models (see https://www.lse.ac.uk/philosophy/blog/2021/02/16/what-are-scientific-models-and-how-much-confidence-can-we-place-in-them/) 

By Luca Zanetti

Luca Zanetti is a Fixed-Term Researcher of Logic and Philosophy of Science at the School for Advanced Studies IUSS Pavia. Previously he held a postdoctoral position in the Dept. of Civil and Environmental Engineering of Politecnico di Milano. He visited the Center for Philosophy of Natural and Social Sciences (CPNSS) at LSE between July and December 2022. His current project concerns normative uncertainty in epistemology, decision theory, and moral philosophy.

Further readings

Dietrich, Franz & Jabarian, Brian (2022). Decision under normative uncertainty. Economics and Philosophy 38 (3):372-394.

Bradley, Richard (2017). Decision Theory With a Human Face. Cambridge University Press.

MacAskill, William; Bykvist, Krister & Ord, Toby (2020). Moral Uncertainty. Oxford University Press.

Marinacci, M. (2015). Model Uncertainty. Journal of the European Economic Association, 13: 1022-1100. https://doi.org/10.1111/jeea.12164

Roussos, Joe (2022). Modelling in Normative Ethics. Ethical Theory and Moral Practice (5):1-25.

Credits

The title picture of this blog article depicts the ‘Belgica’ on the ice. The ship was used for the Belgian Antarctic Expedition of 1897–1899 and was the first expedition to winter in the Antarctic region. The author has chosen this picture because it’s his favourite metaphor for normative uncertainty. About the picture: The BELGICA anchored at Mount William (1989) Copyright: Public Domain